Information Theory and Coding > Error Control Coding > Some Important Definitions on Error Correcting Codes
Some important terms
A Word is a sequence of symbols. A Code is a set of vectors called Codewords.
Example: {0100, 1111} is a set of two codewords
Hamming Weight: Hamming Weight of a Codeword is equal to the number of nonzero elements in the codeword. Example: Hamming Weight of a codeword c1 is denoted by w(c1)=w(1011)=3.
Hamming Distance: Hamming Distance between two codewords is the number of places the codewords differ. Example: Hamming Distance between two codewords c1 and c2 is denoted by d(c1, c2)=d(0100, 1111) =3
Code Rate: The Code Rate of an (n, k) code is defined as the ratio (k/n), and denotes the fraction of the codeword that consists of the information symbols. Code rate is always less than unity. The smaller the code rate, the greater the redundancy, i.e., more of redundant symbols are present per information symbol in a codeword. A code with greater redundancy has the potential to detect and correct more of symbols in error, but reduces the actual rate of transmission of information.
Minimum Distance: Minimum distance of a code is the minimum Hamming distance between any two codewords. An (n, k) code with minimum distance a is sometimes denoted by (n, k, d*). Minimum distance of the above codewords is 2.
Minimum Weight: Minimum weight of a code is the smallest weight of any non[1]zero codeword, and is denoted by w*. Minimum weight of the above codewords is 2.
Repetition Code: Sending the same message several times. In transferring a message if we send a ciode repetitive times the maximum number of times actual code will be received and less number of times errors will occurs.
Example:
Original Message 01010
Repetition code: 000 111 000 111 000
Received message: 010 110 100 101 100
Decoded Message 0 1 0 1 0
Again
Original Message 01010
Repetition code: 000 111 000 111 000
Received message: 010 100 100 101 110
Decoded Message 0 0 0 1 1
If more than 1 one error occur for a 3-bit block, we will get the wrong answer i.e we can only fix 1 error per 3-bits. We have repeated the message 3 times. So our efficiency is 33%.
Parity Bit
A parity bit is a check bit, which is added to a block of data for error detection purposes. Parity bit is used to validate the integrity of the received data.
Example: Original message: 100101
Sending message: 10010111
Last two bits ‘11’ added with the message for validation purpose of received message.
Odd Parity: When total number of 1’s in the message is even then the parity bit value is set to in such a way that the total number of 1’s in the transmitted set (including the parity bit) will be an odd number.
Example: Original message: 110101
Sending message: 11010101
Even Parity: When total number of 1’s in the message is odd then the parity bit value is set to in such a way that the total number of 1’s in the transmitted set (including the parity bit) will be an even number.
Example: Original message: 100101
Sending message: 1001011
Total number of 1’s in the original message is 3. But one extra parity makes total number of 1’s is 4 which is even. So this parity is called even parity.
How many Parity Bit?
The amount of parity data added to Hamming code is given by the formula 2r ≥ k + r + 1, where r is the number of parity bits and k is the number of data bits. For example, if we want to transmit 3 data bits, the formula would be 23 ≥ 3 + 4 + 1, so 3 parity bits are required.
Generation Matrix:
A defined matrix is called a generator matrix, G, which rows will be linearly independent. Thus, a linear combination of the rows can be used to generate the codewords of C. The generator matrix will be a k× n matrix with rank k.
The generator matrix converts (encodes) a vector of length k to a vector of length n. Let the input vector (uncoded symbols) be represented by i. The coded symbols will be given by
C = iG
where c is called the codeword and i is called the information word. The generator matrix provides a concise and efficient way of representing a linear block code.
Example: consider the source codes are {00, 01, 10, 11}
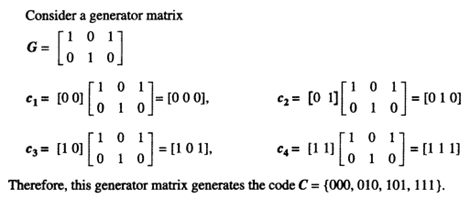
Feedback
ABOUT
Statlearner
Statlearner STUDY
Statlearner