Information Theory and Coding > Data Compression > Explain Arithmetic Coding with example

Arithmetic Coding:

In arithmetic coding technique, a string of characters like the words “hello friends’ is represented using a fixed number of bits per character, as in ASCII code. When a string is converted to arithmetic encoding, frequently used characters are stored with fewer bits and not-so-frequently occurring characters are stored with more bits, resulting in relatively fewer bits used in total.

The steps of arithmetic coding algorithm are:

1. Put the symbols in decreasing order of probabilities p_i i ∈ I p₁ ≥ p₂ ≥···≥ p_m
2. Divide the interval [0; 1) into n intervals of dimensions p_1, p₂ ,···, p_m
3. Read the first symbol of the message and memorise its associated interval.
4. Divide this interval into n intervals, each of them proportional to p_1, p₂ ,···, p_m
5. Read the next symbol and memorise the interval associated to it.
6. Continue the process following the same algorithm.
7. Transmit one number (Lower range) from the last memorised interval

Difference between Arithmetic Coding and Huffman Coding

Arithmetic Coding	Huffman Coding
Complex technique for coding short messages	Simple technique
Gives optimum result	Does not give optimum result
There is no one-to-one correspondence between source symbol and codeword	There is one-to-one correspondence between source symbol and codeword
Compression ratio is more	Compression ratio is less
Execution time is more	Execution time is more

 

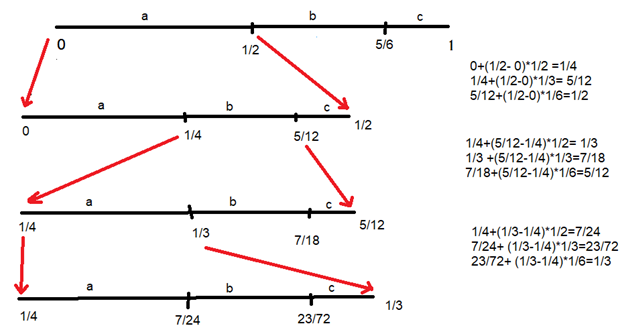
Example: Encode the message “abac” using an arithmetical code designed for the source S and probability of their occurrences are {a,b,c}={ 1/2 , 1/3 , 1/6}. Encode this string using arithmetic coding algorithm.

 

Encoding:

Processed Interval			Read Symbol	Memorised interval
0 - 1/2	1/2 – 5/6	5/6 -1	a	0 – 1/2
0 + (UL –LL)*Pr 0 + (1/2 -0)*1/2 =1/4	1/4 + (1/2 -0)*1/3 = 5/12	1/2
0        – 1/4	1/4  - 5/12	5/12 -1/2	b	1/4  - 5/12
1/4  - 1/3	1/3 – 7/18	7/18 -5/12	a	1/4  - 1/3
1/4  - 7/24	7/24 – 23/72	23/72 - 1/3	c	23/72 -1/3

We may transmit a number from the interval [23/72; 1/3], for example 23/72.

Decoding: 23/72 is received

Processed Interval			Interval Containing 23/72	Associated Symbol
0 - 1/2	1/2 – 5/6	5/6 -1	0-1/2	a
0 + (UL –LL)*Pr 0 + (1/2 -0)*1/2 =1/4	1/4 + (1/2 -0)*1/3 = 5/12	1/2
0        – 1/4	1/4  - 5/12	5/12 -1/2	1/4 -5/12	b
1/4  - 1/3	1/3 – 7/18	7/18 -5/12	1/4  - 1/3	a
1/4  - 7/24	7/24 – 23/72	23/72 - 1/3	23/72 - 1/3	c

 

So decoding string is abac

 

Prev

What is Huffman Coding?

No More

Feedback

Submit